树
数据结构
数据结构分两种:
- 物理结构:内存中真实存在的结构
- 数组
- 链表
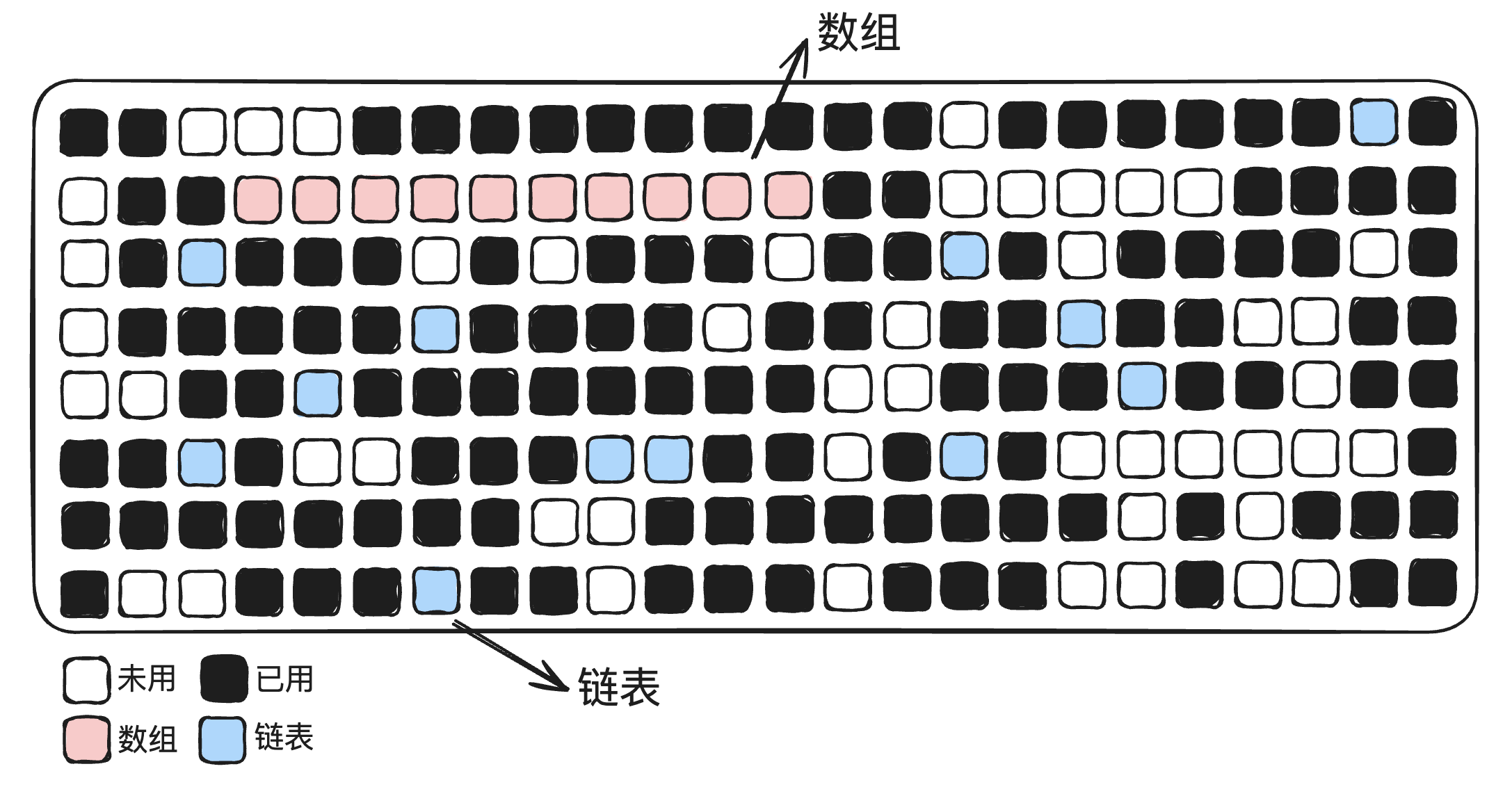
- 逻辑结构
- 线性结构:数组、链表、栈、队列
- 非线性结构:树、图、集合(Set)、字典(Map 不同语言叫法:映射、关联数组、字典、Hash表)
- 这些逻辑结构背后还是使用的数组或者链表去存储的。
DOM树、编译器里面的语法树、数据库索引B+树

- 叶子节点:没有子节点的节点,位于树的末端。
- 兄弟节点:相同的父节点的子节点之间互为兄弟节点。
- 度:一个节点的子节点的个数
树的表示
- 图示法
- 符号法
plain
(A(B (D ,(G, H, I)), C(E(J), F)))树的种类是非常多的:
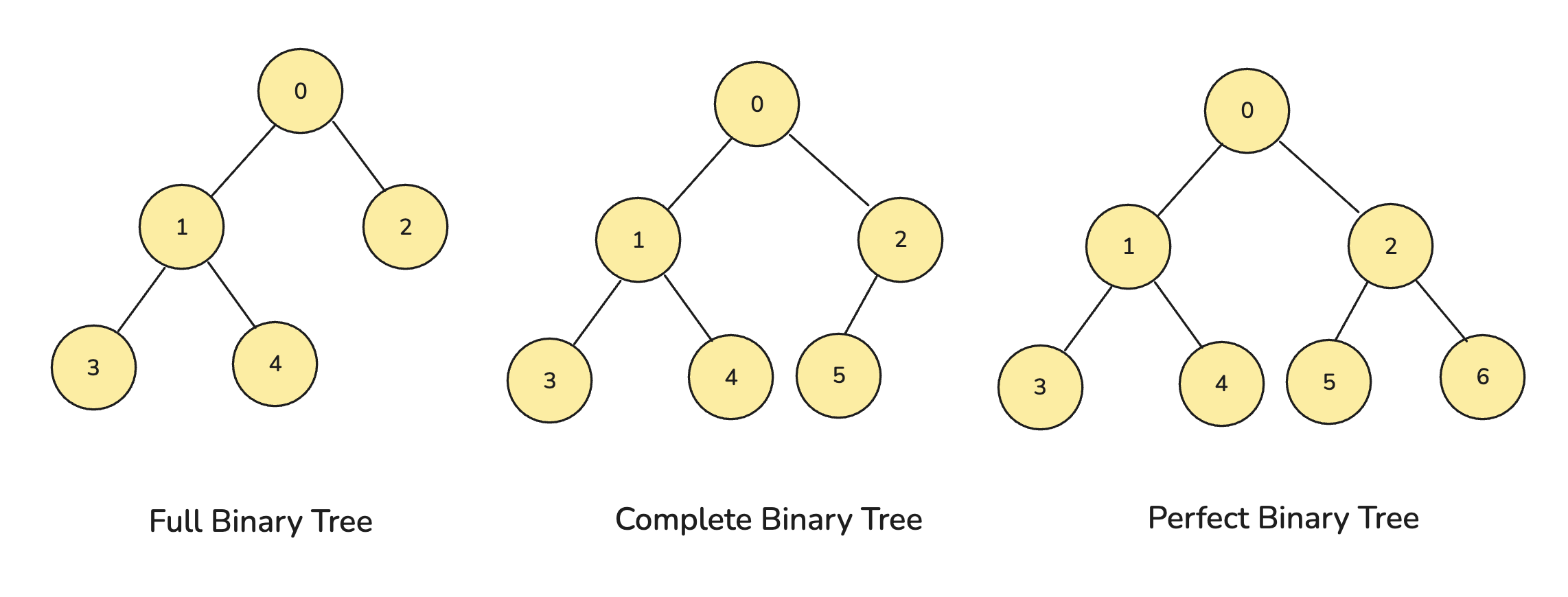
二叉树
- 满二叉树
- 完全二叉树
- 二叉搜索树
- 平衡二叉搜索树(AVL树、2-3-4树、红黑树)
- 二叉堆
多叉树
- B树
- B+树
- 字典树
首选就是二叉树。
子节点最多只能有2个。
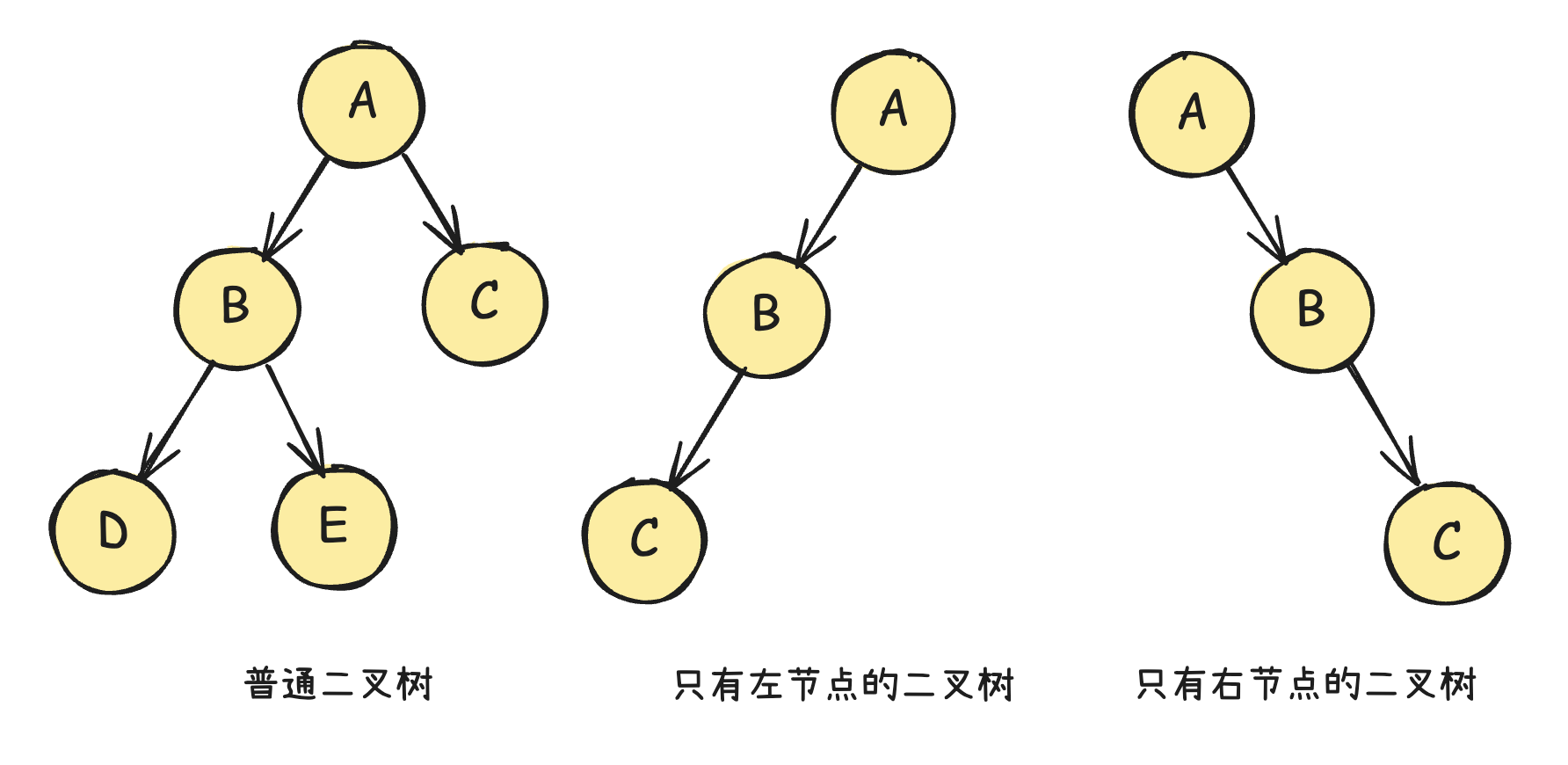
两种特殊结构的二叉树:
- 满二叉树
- 完全二叉树
满二叉树
plain
A
/ \
B C
/ \ / \
D E F G- 第 i 层会有 2^i 个节点
- 如果高度为 h,总节点数 2^{h+1} - 1 个节点
- 叶子节点数量:在高度为 h 的满二叉树中,叶子节点的数量为 2^h
完全二叉树
- 除了最后一层,其他层必须是满的
- 最后一层可以不满,但是所有的节点必须从左往右排列
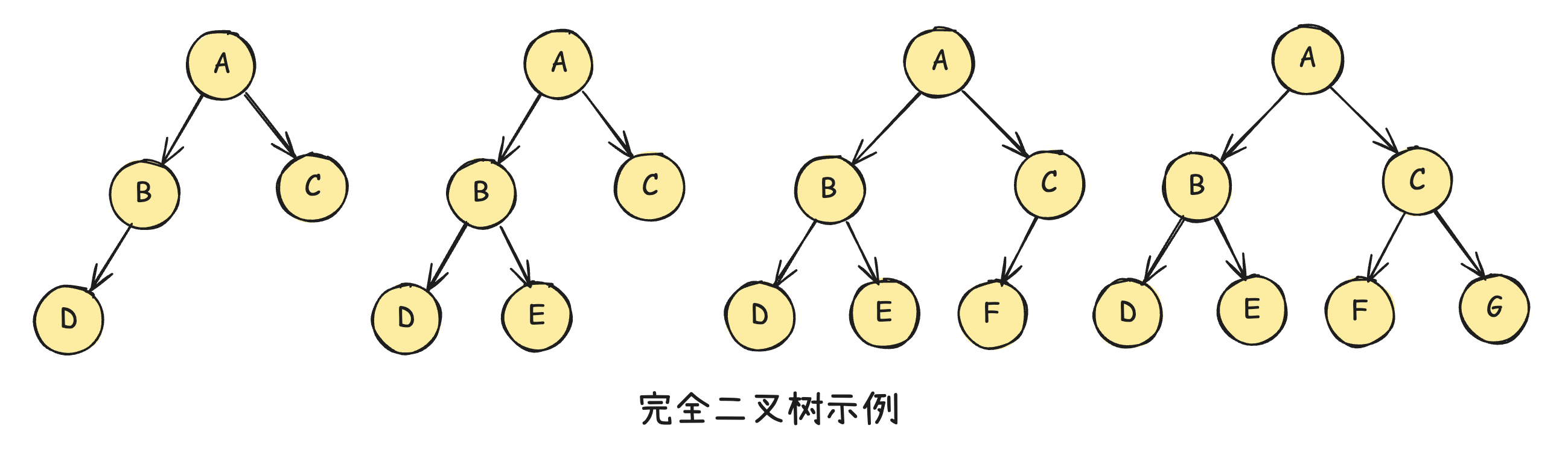
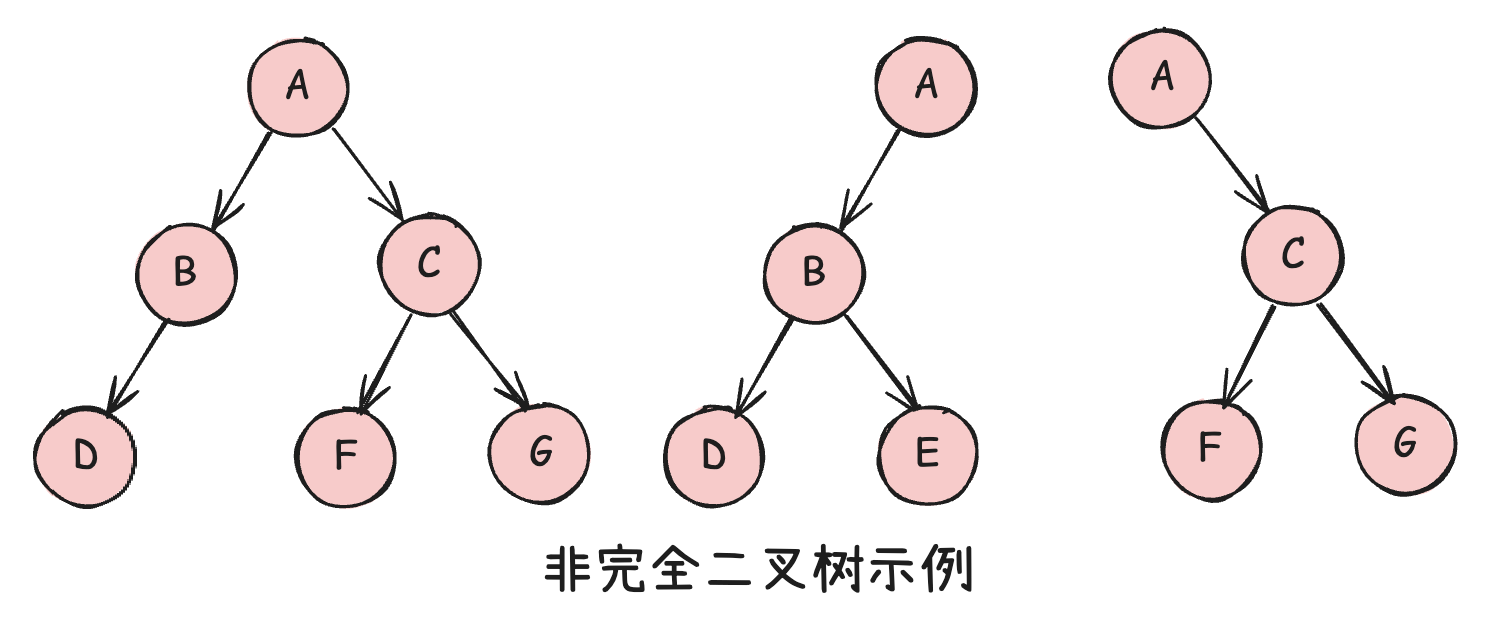
关于满二叉树和完全二叉树,国内外定义不一样。
- 完全二叉树:Complete Binary Tree
- 满二叉树:Perfect Binary Tree
- Full Binary Tree:所有节点要么没有孩子节点,要么有两个孩子节点
二叉树的存储
二叉树一般使用数组来存储,因为用数组可以很方便的找到它的所有亲属
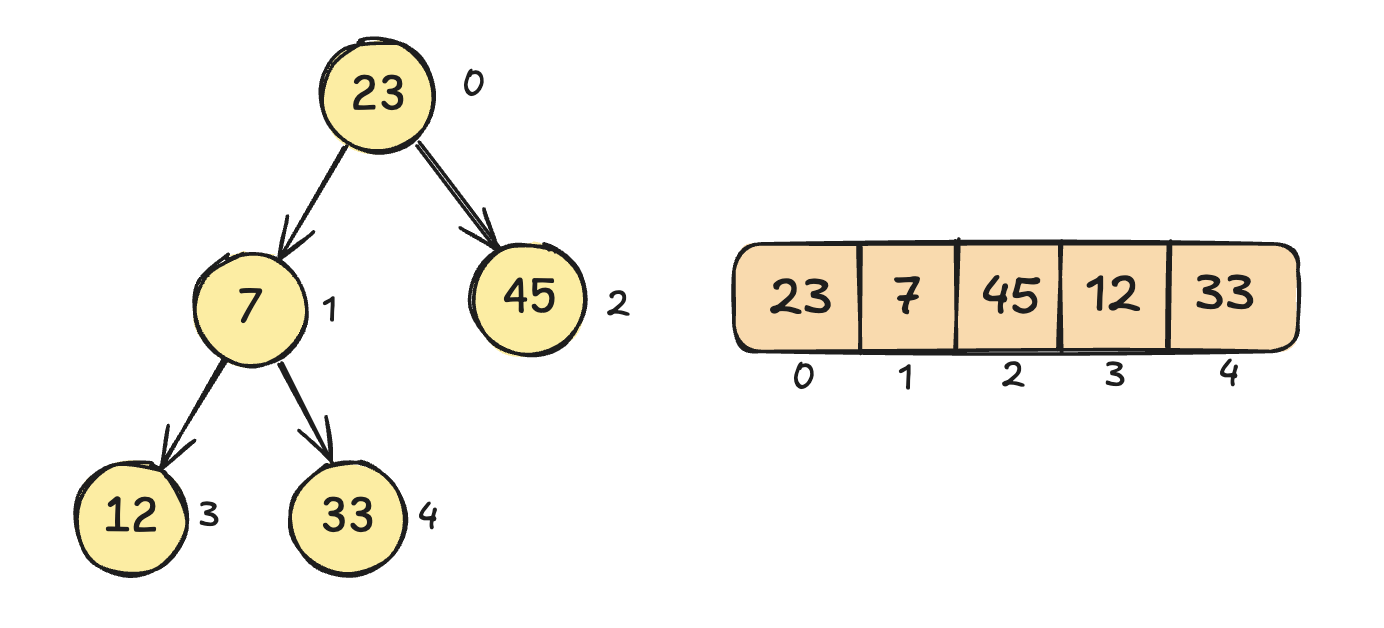
- 找节点的父节点:
Math.floor((index - 1) / 2)- 1 : 0
- 2: 0
- 3: 1
- 4 : 1
- 左子节点:
index * 2 + 1- 0: 1
- 1: 3
- 2: 5
- 右子节点:
index * 2 + 2- 0: 2
- 1: 4
- 2: 6
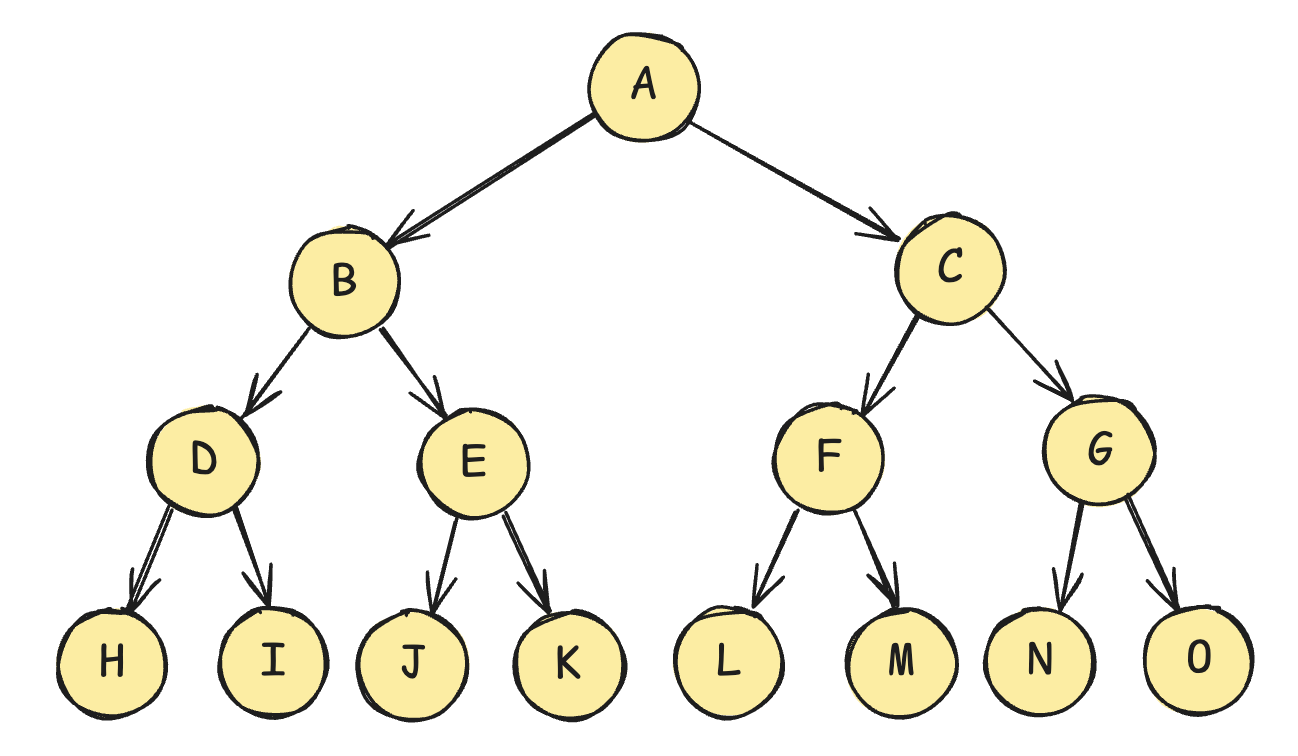
二叉树的遍历
分为三种:
- 前序遍历:根节点 --> 左子树 --> 右子树
- 中序遍历: 左子树 --> 根节点 --> 右子树
- 后序遍历:左子树 --> 右子树 --> 根节点
前序顺序:
plain
A B D H I E J K C F L M G N O中序遍历:
plain
H D I B J E K A L F M C N G O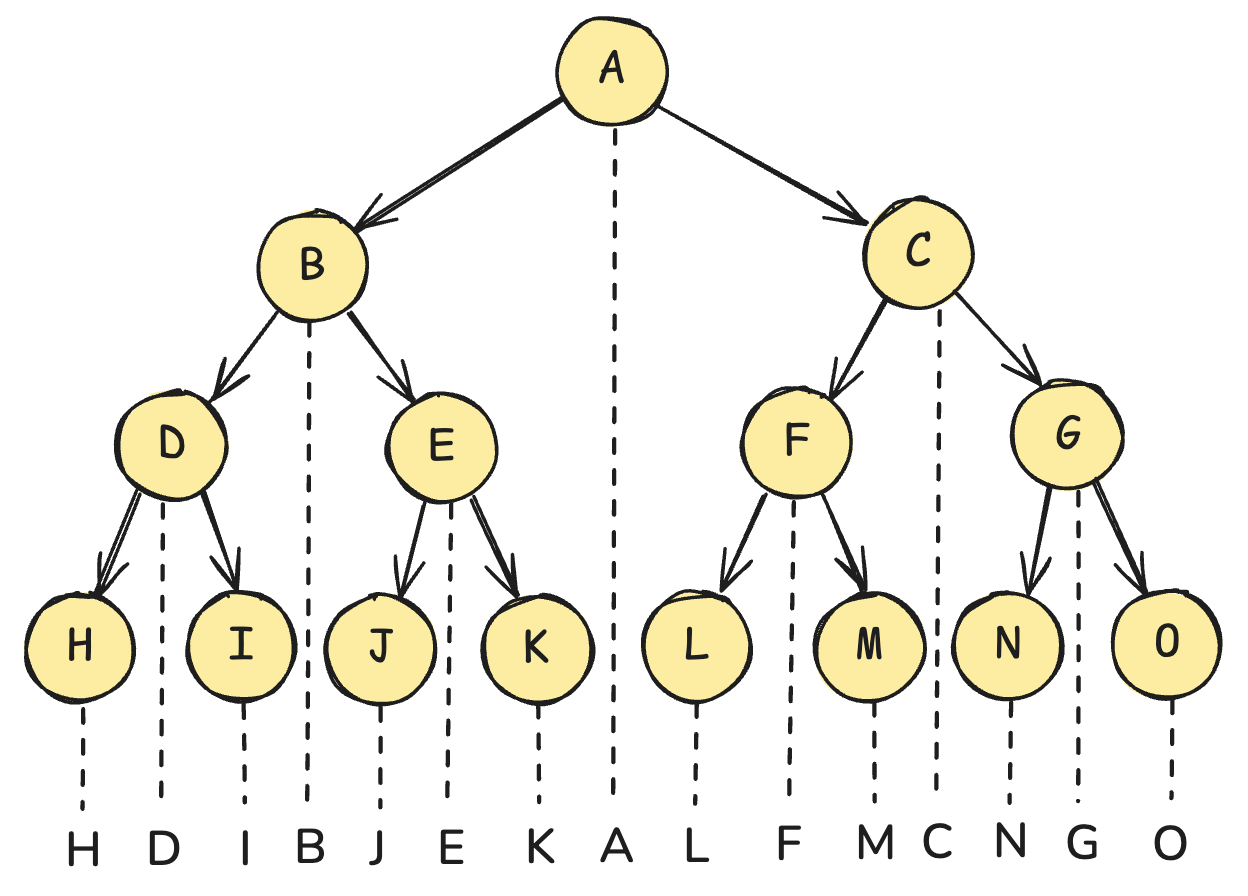
后序遍历:
plain
H I D J K E B L M F N O G C Ajavascript
class TreeNode {
constructor(value) {
this.value = value; // 节点的值
this.left = null; // 左子树
this.right = null; // 右子树
}
}
// 接下来构建整颗二叉树
const root = new TreeNode("A"); // 根节点
root.left = new TreeNode("B"); // 左子节点
root.right = new TreeNode("C"); // 右子节点
root.left.left = new TreeNode("D");
root.left.right = new TreeNode("E");
root.left.left.left = new TreeNode("H");
root.left.left.right = new TreeNode("I");
root.left.right.left = new TreeNode("J");
root.left.right.right = new TreeNode("K");
root.right.left = new TreeNode("F");
root.right.right = new TreeNode("G");
root.right.left.left = new TreeNode("L");
root.right.left.right = new TreeNode("M");
root.right.right.left = new TreeNode("N");
root.right.right.right = new TreeNode("O");
function preOrderTranverse(root){
if(root === null) return;
// 根节点
console.log(root.value);
// 左子树
preOrderTranverse(root.left);
// 右子树
preOrderTranverse(root.right);
}
function inOrderTranverse(root){
if(root === null) return;
// 左子树
preOrderTranverse(root.left);
// 根节点
console.log(root.value);
// 右子树
preOrderTranverse(root.right);
}
function postOrderTranverse(root){
if(root === null) return;
// 左子树
preOrderTranverse(root.left);
// 右子树
preOrderTranverse(root.right);
// 根节点
console.log(root.value);
}
preOrderTranverse(root);看一个查找的场景。
javascript
// 假设有 10000 个乱序的数,查找指定的元素
const arr = [];
for(let i = 0; i < 10000; i++){
arr[i] = Math.floor(Math.random() * 10000);
}
function search(arr, target){
for(let i = 0; i < arr.length; i++){
if(arr[i] === target) return true;
}
return false;
}
console.log(search(arr, 7));- 算法
- 数据结构
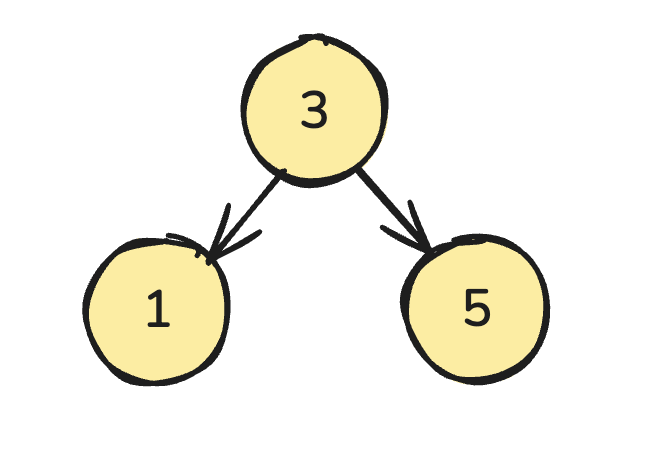
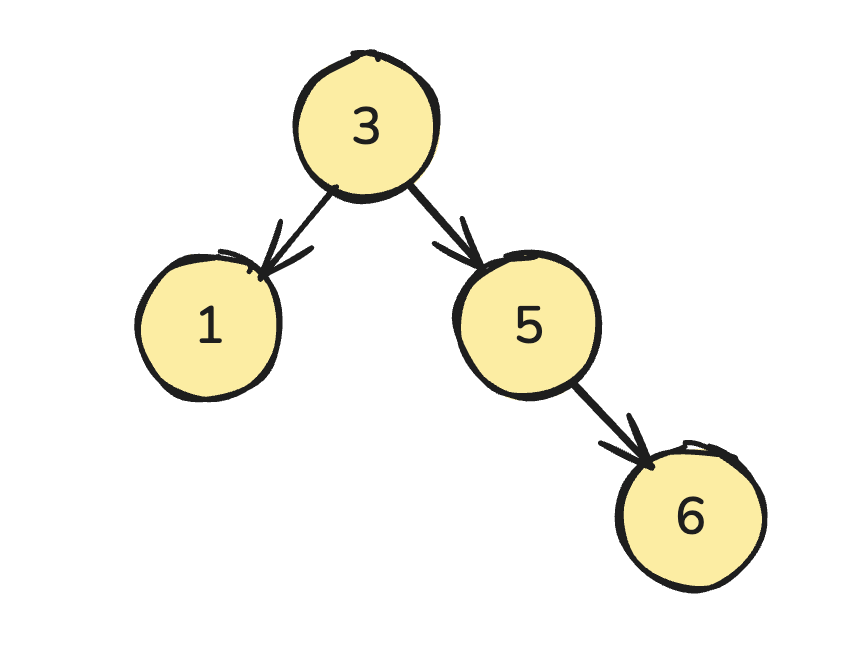
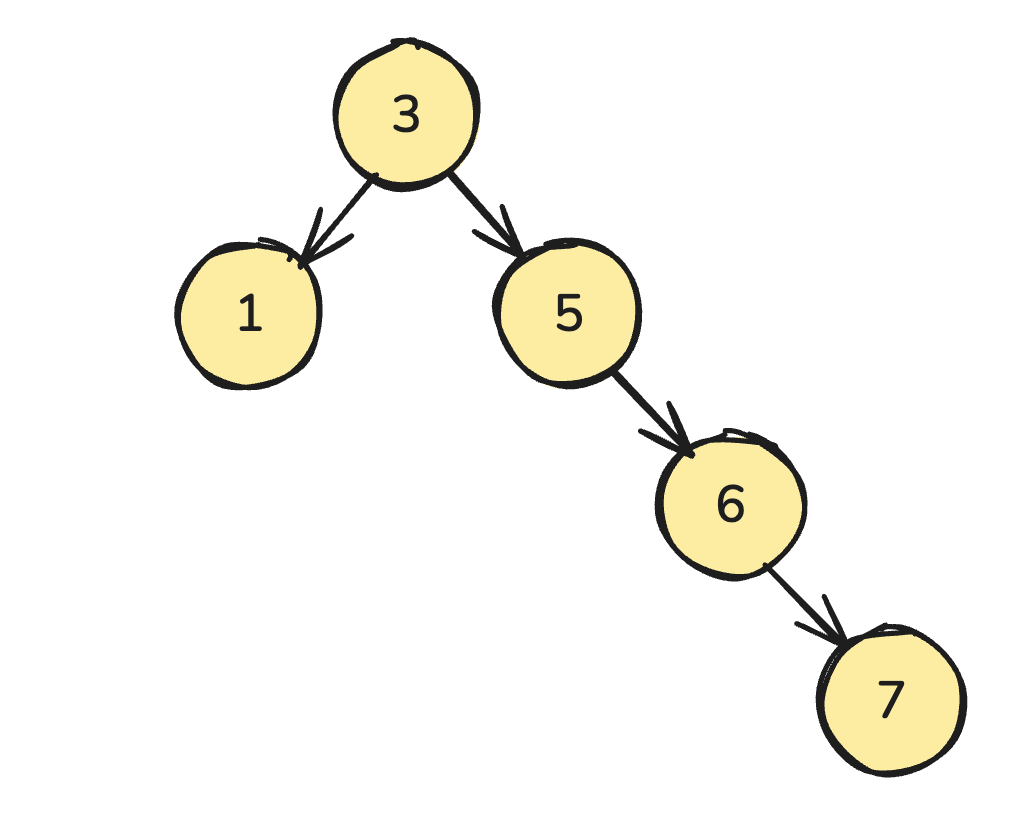
这里可以将这 10000 个形成一颗二叉搜索树(Binary Search Tree,BST)
plain
[3, 5, 1, 6, 7, 2, 9, 8]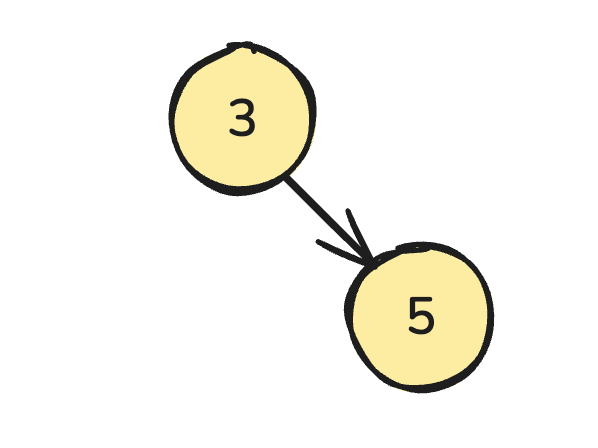
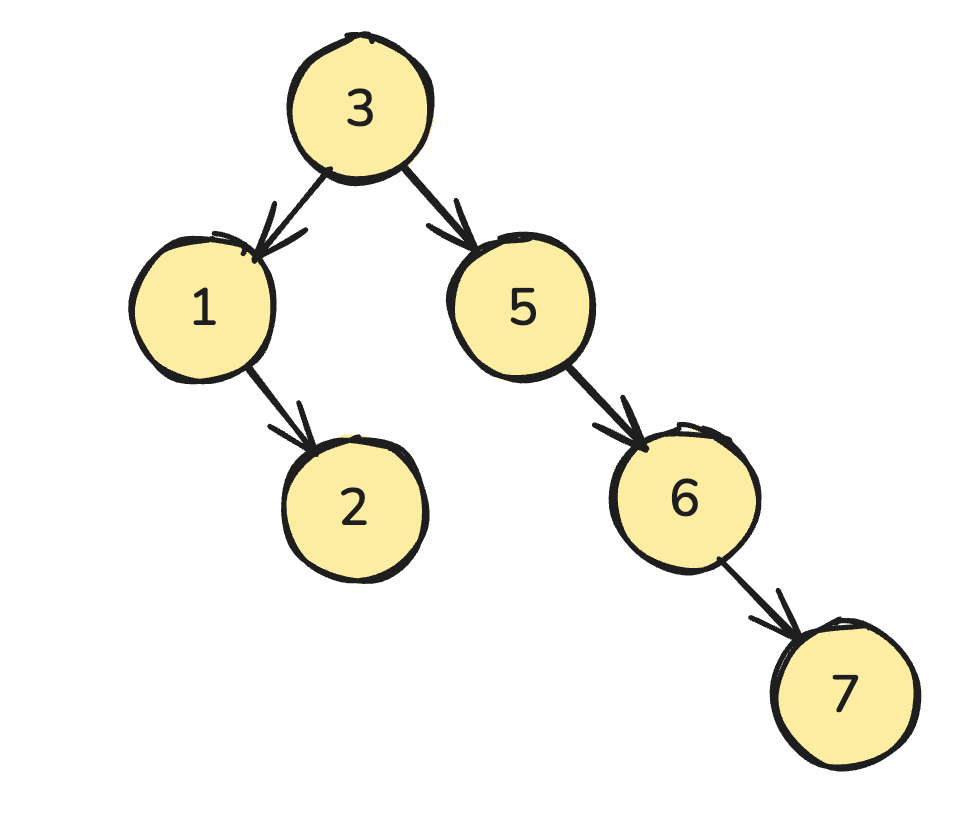
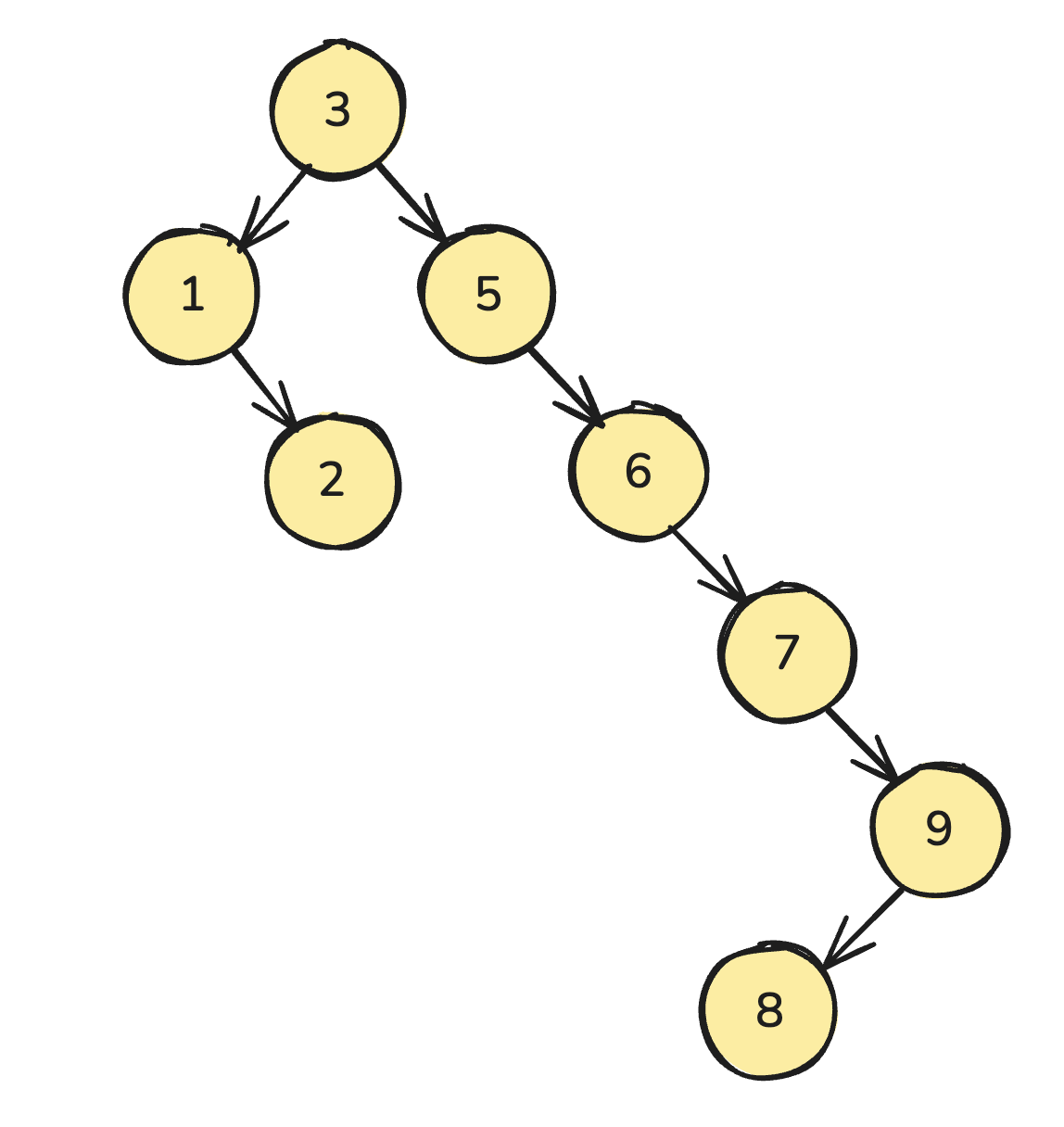
javascript
class TreeNode{
constructor(value){
this.value = value;
this.left = null;
this.right = null;
}
}添加节点的方法:
javascript
function addNode(root, num){
if(root === null || root.value === num) return;
if(root.value < num){
// 说明目标值比当前节点大
if(root.right === null) root.right = new TreeNode(num);
else addNode(root.right, num);
} else {
// 说明目标值比当前节点小
if(root.left === null) root.left = new TreeNode(num);
else addNode(root.left, num);
}
}接下来来创建 BST 树
javascript
function buildSearchTree(arr){
if(arr === null || arr.length === 0) return null;
const root = new TreeNode(arr[0]);
for(let i = 1; i < arr.length; i++){
addNode(root, arr[i]);
}
return root;
}还需要一个搜索的方法
javascript
function searchByTree(root, target){
if(root === null) return false;
if(root.value === target) return true;
if(root.value > target) return searchByTree(root.left, target);
else return searchByTree(root.right, target);
}-EOF-
